¶ Summary
- The goal is to develop an assistant for solving the popular Mastermind game, implemented as an expert system. **Instead of encoding a complex algorithm**, the approach relies on a clear **set of facts and simple game rules** forming a knowledge base. A deductive engine utilizes this base to make informed guesses about the secret code. Further guesses feed the knowledge base.
- A user-friendly interface is needed to facilitate interactions with the engine: defining game rules, exchanging guesses and feedback, tuning performance and strategy, and supporting debugging and testing. Initial exploration of a full Python stack revealed a lack of suitable logic programming engines for this purpose.
- While Jupyter Notebook, with its embedded visualization and analytics functions, is chosen to implement the interaction and analysis layer, an open-source Java-based logic programming engine is found and adopted for the deductive engine. To achieve interoperability, the java engine is embedded within a servlet, exposing it as a web application. A Python REST client is developed to communicate with this backend, creating an interactive, cross-technology system driven by deductive reasoning.
- The resulting system supports seamless user interaction and rule-based inference. Beyond solving the game, a prescriptive analytics process is designed to benchmark various game strategies, identifying the one that consistently cracks the secret in the fewest moves.
¶ Methodology used
We present the project execution in accordance with the CRISP-DM framework .
¶ The business issue
¶ background
We want a digital assistant that help us solve the Mastermind board game. On the board, once the 'codemaker' sets a secret combination of colored pegs, we, the 'codebreakers', start an iteration of guesses by proposing our combination of pegs and receiving a feedback that confirms, with respect to the secret combination, how many pegs are in the right position and how many are there but in the wrong position. We make new new, more informed guesses by considering the knowledge we acquire on the go. That is what the digital assistant will do for us.
¶ objectives and success criteria
We want to build a model that follows a strategy that minimize the number of guesses needed to crack the secret.
¶ data mining goals
from a technical standpoint, we want to have measurable evidence that the strategy we eventually choose is statistically better than other strategies.
¶ project plan
We will have to setup a user-friendly environment to develop, test, tune and use the model.
We will use Jupyter Notebook to build, test and use with python.
We will choose an engine that will either be a python library or an easy-to-use RESTful API.
¶ The chosen technology
- The solution of many combinatorial games are often implemented through a recursion algorithm in a program that follows the imperative paradigm (Java, Python).
- recursions might sometimes have high memory requirements and are not trivial to code, to read and to maintain. Moreover, in this case, we should be coding two nested recursions [1]
- The declarative paradigm of logic programming offers the opportunity, only for a limited types of problems, to completely specify the behaviour of a problem solver through the definition of a few, clear rules. The actual steps, triggered by a simple query, are executed by the logic Engine behind the scenes.
A notable advantage of the logic programming paradigm is that
it is explainable / white-box, thus falling into the 'XAI' domain. [2]
- The two most popular languages and engines seem to be Prolog and Datalog.
- We wanted to test an implementation in Datalog, a pure declarative paradigm. [3]
- After searching for a python implementation of Datalog, we found pyDatalog which unfortunately does not seem to support, at the time of evaluation, writing rules in pure Datalog language.
- We then opted for a java, robust, pure Datalog implementation: the HarvardPL AbcDatalog.
- Given that we want to stick to a Jupyter Notebook user interface, we will create a stack with:
- the original datalog implementation
- a small ad hoc wrapper that implement a stateful Datalog-as-a-service engine with an http REST interface.
- a python notebook user interface.
¶ The data
The size of the combination and the number of available colors are both fixed upfront. In our case, we go for games with four pegs that may assume six colors.
The secret and the guesses must both have all four pegs with any of the six available colors.
The data in this project is generated and not acquired, so there is no data preparation phase.
We will base our tests on a couple of secrets that will verify that the game feedbacks are properly taken into account while formulating the next guesses.
¶ Modeling
This is a combinatorial optimization problem and we are going to use the Branch-and-Bound method.
The application of a fixed set of logic rules to the guess-and-feeback history will rule out more and more combinations. After that, we will pick one of the survived combinations. We want to better understand if there is a good way and a bad way to choose a survived combination for our next guess.
¶ The implementation of the business rules in Datalog
The code below covers the key facts and rules of the business logic.
The full set is available at https://github.com/a-moscatelli/home/tree/main/am-wiki-assets/logicprogramming/datalog-kb
glossary:
- ho = 4 holes: h0 to h3
- co = 6 guess colors: c0 to c5
- black, white, not-given: original feedback set, non-positional.
A note on extensibility.
In this implementation, changing the number of colors requires the change of one line of code.
Changing the number of holes, on the other side, which is a structural property, requires a more extensive code adaptation.
% mmind-datalog---entities.ps BEGIN
%holes:
isa(h0,ho). isa(h1,ho). isa(h2,ho). isa(h3,ho).
%peg colors:
isa(c0,co). isa(c1,co). isa(c2,co). isa(c3,co). isa(c4,co). isa(c5,co).
%feedback peg colors:
isa(b,fb). isa(w,fb). isa(o,fb).
% sequencing
follows(h1,h0,ho). follows(h2,h1,ho). follows(h3,h2,ho).
% mmind-datalog---entities.ps END
Above,
- h1 follows h1 in the sequence of holes, etc.
- c0 is a color, h1 is a hole, etc.
a data model based on facts likeisa(c0,co)rather than facts defined asisacolor(c0), provides the opportunity to implement universal definition of permutation(), product(), combination() and follows() rules that can be applied to any class.
% mmind-datalog---itertools.ps BEGIN
% OC = class
itertools_product4(X0,X1,X2,X3,OC) :- isa(X0,OC), isa(X1,OC), isa(X2,OC), isa(X3,OC). % sz = 1296 = NOC**NOH
% the rules based on follows are only valid when at least one follows() is defined ie when at least two items exist.
isNotTheOnly(X1,OC) :- isa(X1,OC), isa(X2,OC), X1 != X2.
isTheOnly(X0,OC) :- not isNotTheOnly(X0,OC), isa(X0,OC).
isNotTheFirst(X2,OC) :- follows(X2,X1,OC).
isNotTheLast(X1,OC) :- follows(X2,X1,OC).
isTheFirst(X1,OC) :- follows(X2,X1,OC), not isNotTheFirst(X1,OC).
isTheFirst(X1,OC) :- isTheOnly(X1,OC).
isTheLast(X2,OC) :- follows(X2,X1,OC), not isNotTheLast(X2,OC).
isTheLast(X1,OC) :- isTheOnly(X1,OC).
% mmind-datalog---itertools.ps END
The above are general Combinatorics rules. The rules to generate Combinations are given as flat definitions based on ordered items, hence the dependency on the follows() rule, while the Permutations are defined through a tree-like divide-and-conquer rule-set.
% mmind-datalog---bizlogic.ps BEGIN
itertools_permutations_fb(GID, H0P,H0, H1P,H1, H2P,H2, H3P,H3) :-
isa_validfb2vert(GID, H0P,H0),
isa_validfb2vert(GID, H1P,H1),
isa_validfb2vert(GID, H2P,H2),
isa_validfb2vert(GID, H3P,H3),
H0P != H1P, H0P != H2P, H0P != H3P,
H1P != H2P, H1P != H3P,
H2P != H3P.
% projection
isa_feedbackpermut(GID,H0,H1,H2,H3) :- itertools_permutations_fb(GID, H0P,H0, H1P,H1, H2P,H2, H3P,H3).
% head(3):
% isa_feedbackpermut(g0, p3, x, p1, w, p0, b, p2, w)
% isa_feedbackpermut(g0, p1, w, p3, x, p2, w, p0, b)
% isa_feedbackpermut(g0, p3, x, p0, b, p1, w, p2, w)
isa_solution_exante(CH0,CH1,CH2,CH3) :- itertools_product4(CH0,CH1,CH2,CH3,co).
isa_validguess_evenafter_gid(GID,CH0,CH1,CH2,CH3) :-
isa_validatedGuess(GID,GC0,GC1,GC2,GC3),
isa_feedbackpermut(GID, H0, H1, H2, H3),
isa_solution_exante(CH0,CH1,CH2,CH3),
isa_121match(GC0,H0,CH0),
isa_121match(GC1,H1,CH1),
isa_121match(GC2,H2,CH2),
isa_121match(GC3,H3,CH3),
isa_12anymatch(GC0,H0,CH0,CH1,CH2,CH3),
isa_12anymatch(GC1,H1,CH0,CH1,CH2,CH3),
isa_12anymatch(GC2,H2,CH0,CH1,CH2,CH3),
isa_12anymatch(GC3,H3,CH0,CH1,CH2,CH3).
isa_121match(GCX,HX,CHX) :- isa(GCX,co), isa(HX,fb), isa(CHX,co), GCX = CHX, HX=b.
% ... etc
isa_12anymatch(GCX,HX,CH0,CH1,CH2,CH3) :- HX=w, GCX = CH0, isa_solution_exante(CH0,CH1,CH2,CH3), isa(GCX,co).
% ... etc
isa_12anymatch(GCX,HX,CH0,CH1,CH2,CH3) :- HX=b, isa_solution_exante(CH0,CH1,CH2,CH3), isa(GCX,co).
isa_12anymatch(GCX,HX,CH0,CH1,CH2,CH3) :- HX=o, isa_solution_exante(CH0,CH1,CH2,CH3), isa(GCX,co).
isa(GG,CL) :- isa_validatedGuess(GG,_,_,_,_), CL=gg.
% when a user submits : api_isa_guess(g0,c0,c0,c0,c1). then you must accept that g0 is a gg.
% gid = guess label (example: g3)
% recursive:
isa_validguess_evenafter_gg_upto_gid(GID,CH0,CH1,CH2,CH3) :- isa_validguess_evenafter_gid(GID,CH0,CH1,CH2,CH3), isa_validatedGuessWithFback(GID), isTheFirst(GID,gg).
isa_validguess_evenafter_gg_upto_gid(GID,CH0,CH1,CH2,CH3) :- isa_validguess_evenafter_gid(GID,CH0,CH1,CH2,CH3),
follows(GID,LOWERGID,gg),
isa_validguess_evenafter_gg_upto_gid(LOWERGID,CH0,CH1,CH2,CH3).
% mmind-datalog---bizlogic.ps END
% mmind-datalog---queries.ps BEGIN
% reading API:
api_isa_validguess_evenafter_all_gg(CH0,CH1,CH2,CH3) :-
isa_validguess_evenafter_gg_upto_gid(GID,CH0,CH1,CH2,CH3),
isa_validatedGuessWithFback(GID),
isTheLast(GID,gg).
% mmind-datalog---queries.ps END
The user "that seeks assistance" is expected to submit this query:
api_isa_validguess_evenafter_all_gg(CH0,CH1,CH2,CH3)?
The user, after each attempt, will add further information to the KB in this format (below is an example of guess and feedback #g2):
% guess #1 with id = g0:
api_isa_guess(g0,c0,c0,c0,c1).
isa_fback(g0,b,w,o,o).
% guess #2 with id = g1:
api_isa_guess(g1, c0, c5, c5, c5).
isa_fback(g1,b,w,w,o).
follows(g1,g0,gg).
the datalog rules above may be merged with this script:
set TARGET=mm-dtlg.ps
copy /Y /B mm-dtlg---*.ps %TARGET%
rem TARGET is the initial KB text that is submitted to the engine.
The datalog engine tolerates duplicated terms and duplicated rules and is not sensitive to their order.
Polymorphism applies to facts and rules.
¶ The web service based on the HarvardPL AbcDatalog engine
The HarvardPL AbcDatalog is a standalone desktop application. We will wrap it in a servlet that we will deploy onto a servlet container to obtain a web application.
¶ The RESTful API of the engine
curl -X POST -d '{"kb":"after(a,b). before(X,Y):-after(Y,X)."}' http://localhost:8080/AbcDatalogREST
to append facts and rules to the engine's KB, initially empty.
return codes: 201, 500, 501.
curl -X DELETE http://localhost:8080/AbcDatalogREST
to delete the engine's KB.
return codes: 200, 204, 500.
curl -X GET http://localhost:8080/AbcDatalogREST
to get info about the KB (size and timestamps).
return codes: 200, 204, 500.
curl -X GET http://localhost:8080/AbcDatalogREST?rule=before%28X%2CY%29
to submit a query "before(X,Y)?".
expected answer: "before(b,a)"
return codes: 200, 204, 500, 501.
¶ The concurrency management logic in our servlet
We want to prepare the service for a multi-user usage.
The update of the Knowledge Base and the queries are a shared memory area that must be protected from inconsistencies. Who submit queries should receive a result that is either coming from the old full Knowledge Base or the new full Knowledge Base and not from anything in between.
- the engine java desktop application was taken from
https://github.com/HarvardPL/AbcDatalog
https://harvardpl.github.io/AbcDatalog/ - the ad hoc engine servlet wrapper
https://github.com/a-moscatelli/home/blob/main/am-wiki-assets/logicprogramming/datalog-as-a-service/webapp1/src/main/java/HelloWorld.java
the servlet wrapper mimics the AbcDatalog class:
https://github.com/HarvardPL/AbcDatalog/blob/master/src/main/java/edu/harvard/seas/pl/abcdatalog/engine/EngineExample.java
- the maven project
https://github.com/a-moscatelli/home/blob/main/am-wiki-assets/logicprogramming/datalog-as-a-service/webapp1/pom.xml
the container is deployed in jetty or in winstone (a compact servlet container shipped with Jenkins):
rem Windows batch file
set APPDIR=webapp1
cd %APPDIR%
call mvn package
goto start_winstone
:start_winstone
java -jar .\ext-libs\winstone-0.9.10.jar --commonLibFolder=ext-libs --httpPort 8080 --warfile .\%APPDIR%\target\my-web-app-1.0.0.war
goto end
:start_jetty
java -jar .\ext-libs\jetty-runner-9.4.0.M1.jar --port 8080 .\%APPDIR%\target\my-web-app-1.0.0.war --jar .\ext-libs\AbcDatalog-0.6.0.jar
goto end
:end
¶ The python user interface
The python notebooks import the definition of the RESTful servlet http client:
class ExpertSystem():
...
def submitkb(self,datalog_text):
# POST
...
def resetkb(self):
# DELETE
...
def getkbstat(self):
# GET /
...
def submitquery(self,query):
# GET /?rule=X
...
full code here:
https://github.com/a-moscatelli/home/blob/main/am-wiki-assets/logicprogramming/python_restful_client/mmind.py
¶ Evaluation
We have two layers.
In the first layer, we have an digital assistant that performs the branch-and-bound and, after each feedback, will propose a narrower search space. We, the assisted user, will pick one of the allowed solutions as a next guess to sumbit to the codemaker.
In the second layer, for each of the game strategies we were able to think of, we run a stochastic simulation in which the whole game is automated: the first guess is random (but conforms to the chosen strategy) and picking one of the subsequent guesses from the allowed solutions is also made by following the chosen strategy.
¶ The prescriptive analytics model: simulate with different strategies
The goal of the game solver is to narrow down the acceptable options given the black/white feedbacks collected after each guess.
Every guess will be a pick from the acceptable options and will have a pattern that we call here platykurtic, mesokurtic and leptokurtic by taking the liberty of borrowing the names used to describe the tailedness of continuous distributions:
- we call a guess like red-red-red-red or red-red-red-blue leptokurtic - a low-entropy combination with a very dominant mode: monochromatic or almost monochromatic,
- we call a guess like red-blue-green-magenta platykurtic - a high-entropy combination: like a rainbow,
- we call a guess like red-red-blue-blue mesokurtic - a middle-entropy combination.
Given that our KPI is "average number of guesses needed to solve a game" and our goal is to keep the KPI as low as possible,
we want to check if the solver performs better by choosing a leptokurtic, mesokurtic or platykurtic option at each round.
We also consider a 'just-pick-the-first-option' strategy for benchmarking. We may consider this strategy equivalent to a random picking.
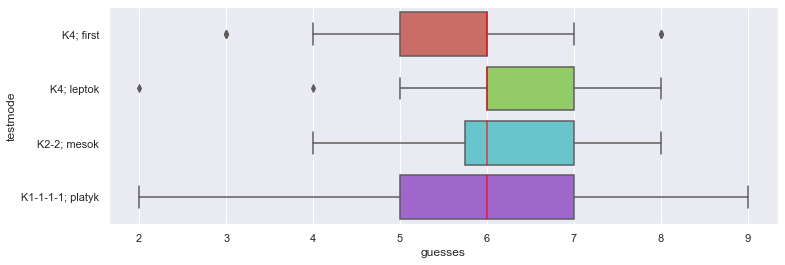
the boxplots above are based on data available at this link:
https://github.com/a-moscatelli/home/blob/main/am-wiki-assets/logicprogramming/second-game-crackingloop/run2/mmind_games_log.tsv
The sample size is 1/18th of the population size = 46.
The logic rules implemented in our engine are pretty good but not the best possible rule set.
The conclusion we can draw from the statistics above, based on the implemented rules, are quite clear:
the PICK-THE-FIRST-OPTION strategy seems to be the best performing strategy.
This strategy is likely close to a PICK-AN-OPTION-AT-RANDOM.
¶ The t-test
Given that we have observed a sample (1/18) of the population of all the games, we want to know if we can confidently proclaim a clear winner among the four strategies we have defined, so we t-test whether the means of two independent samples of number_of_guesses are significantly different:
normality-test
| dataset | sample size | variance | shapiro test |
|---|---|---|---|
| first | 72 | 1.56 | ~not gaussian (p-value=0.000) |
| mesok | 72 | 0.92 | ~not gaussian (p-value=0.000) |
| platyk | 72 | 2.21 | ~not gaussian (p-value=0.003) |
| leptok | 72 | 1.02 | ~not gaussian (p-value=0.000) |
t-test
| ttest_ind | p-value | conclusion |
|---|---|---|
| mesok-platyk | 0.6 | ~same |
| leptok-mesok | 0.4 | ~same |
| leptok-platyk | 0.24 | ~same |
| first-mesok | 0.02 | ~different |
| first-platyk | 0.17 | ~same |
| first-leptok | 0.003 | ~different |
(NB p-value is underestimated if variances are different)
summary:
- first is significantly different from mesokurtic and leptokurtic.
- the other distributions are similar.
NB t-tests assumptions on same variance and gaussian distribution are not met for all samples
¶ Deployment
In the final deployment, we, the 'codemakers', will open a Jupyter Notebook and we think of a secret, then we start the program that will propose a series of guesses to which we reply with our back-and-white feedbacks until the program manages to crack the secret.
¶ The end-user process
The three actors are:
- the Expert system (Datalog Engine embedded inside a Java Web application + Python Client)
- the User
- a M/M game App (a codemaker)
¶ use case 1: the user is an assisted codebreaker
- A knowlege base KB with facts and rules is loaded into the engine and the user starts the M/M App game which creates a secret that will be found with the support of the digital assistant.
- The user specifies, in a M/M App, an initial guess (a set of ordered, colored pegs).
- The M/M App returns a feedback (a set of unordered, black, white and null pegs).
- The user updates the KB of the Assistant with the last guess submitted to the App and the last feedback received from the App.
- The Assistant suggests a new informed guess after considering the previous information added to the KB and by following the 'best strategy'.
- The user specifies, in the App, the suggested guess.
- Steps 3. to 6. are repeated until the App confirms that the last guess matches the secret in step 3.
¶ use case 2: the user is a codemaker
- A knowlege base KB with facts and rules is loaded into the engine
- The user sets a secret that will be found by the digital assistant.
- The digital assistant makes an initial guess (a set of ordered, colored pegs)
- The user submits a feedback (a set of unordered, black, white and null pegs). That will update the KB of the assistant.
- The digital assistant makes another guess after considering the previous information added to the KB and by following the 'best strategy'.
- Steps 4. to 5. are repeated until the assistant returns the only combination left.
¶ A demo run
The python notebook with a complete game is here:
https://ampub.s3.eu-central-1.amazonaws.com/am-wiki-js/logicpro/using_my_rest_abcdatalog_as_an_assistant.html

picture taken from the App used for the simulation - https://www.microsoft.com/en-us/p/mastermind-classic/9wzdncrdpbbx
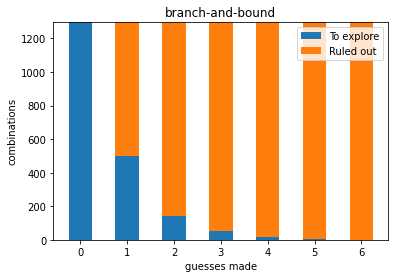
evolution of the search space of the possible options:
evolution of the recompilation time of the knowledge base:
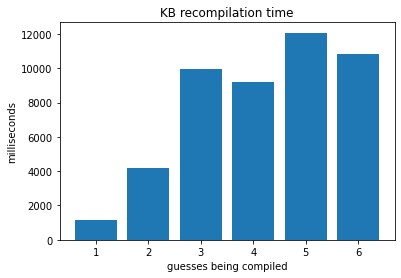
NB - the QUERY response time of the engine is almost flat and less than 5 ms.
¶
Back to Portfolio
¶
one level of recursion is needed to make hypoteses on the holes the a-positional feedback colors refer to, and a second level is needed to make hypoteses on the holes the pegs assumed white in the first recursion should have been instead. ↩︎
https://en.wikipedia.org/wiki/Explainable_artificial_intelligence ↩︎